スチュアートリトルのメッセージ

久しぶりの記事で少々恥ずかしいです。実は全面回復でバリバリ書くにはほど遠いのですが、今日は是非書かねばという気分での復帰です。

スチュアートリトルを知らない方に簡単に筋をお話しします。この映画は、中流クラスの白人家庭の一人っ子の気弱な男の子が、弟が欲しいと言うので両親が施設を訪ねて、養子をつれて帰った。ところが、その弟はなんと、小さな白いネズミだった！というあり得ない話！荒唐無稽な設定だけど、家族鑑賞向けに演出されているのでほのぼのとしていてなかなか楽しい映画だと思います。

でも、僕はこの映画はそれだけではないように思っています。これから見る人には申し訳ないですが、少しだけ映画の中身を話します。

この白いネズミが、施設で両親と初めて出会うとき、「誰も僕を欲しいと言ってくれないんだ...」とかの台詞があるんですが、この主人公の白いネズミが、アフリカ系の少年と置き換えたらどうでしょう？　そう考えるとしっくり来るんです。

実は、他にもそれを感じさせる場面が幾つもあるんです。だから、制作者、脚本家、監督などの人たちは、白い小さなネズミに大きなメッセージを持たせてこの映画を撮ったのだと確信しています。

アメリカには、負の歴史をしっかりと受け止めて子どもたちにそれを伝えようと熱い思いで映画を撮っている人がいるんだと思うと嬉しくなります。

あるいは、僕の勝手な深読みかも知れません。百聞は一見にしかず、2月10日に放映されるはずですので御覧になって下さい。

蛇足ですが実は、アメリカ合衆国にとって2月は、「Black History Month」（「アフリカ系アメリカ人歴史月間 」または「黒人史月間」）です。確かこの呼び方は教育関係者から普及したとか、「差別を無くす」と言う重たい問題を、家庭や学校あるいは地域でしっかり子どもたちに伝えていくことは日本でも大切ですね。

小学校に学ぶグラフ

グラフは、量の差異を視覚的に表す手段。だからグラフを使えば直感的に理解できることが多いと信じて来た。しかし最近ではその僕なりの定説がゆらぎつつある。

例えば、２次不等式の解を２次関数のグラフを用いて求める方法は、x軸より上方（または下方）にグラフの存在するxの値の範囲を求めればいいはずだが分からない生徒が増えている。

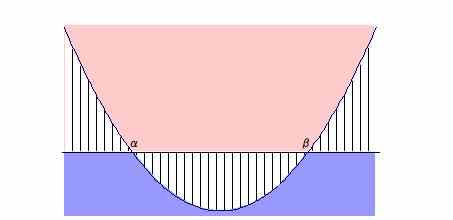
そんな生徒は、一言で言えばグラフを読み取ることができないのだろう。なぜそうした力をつけることができなかったかの理由は色々考えられるが、力が不足しているならそれなりに力を伸ばしてあげたいと考えている。

そんな折り、小学校３年生の棒グラフの授業実践を知った。

＜実践＞
(1)クラス全員に大きめでカラーの付箋を1枚ずつ配布して、好きな教科名を書かせる。

(2)回収して黒板に貼った画用紙に張り出す

(3)「どの教科が1番多いかな？」と発問する

(4)分かりにくいことを合意できたらどうしたらよいか考えさせる

(5)集計すれば良いことを確認したら集計用紙を全員に配布する

(6)教員が付箋に書かれた教科名を1枚ずつ読み上げながら黒板に教科別で正の字を書いていく。そして、読み上げた付箋を下図のように張り並べていく。

(7)全て読み上げたら、教科別の合計数を書き込む。

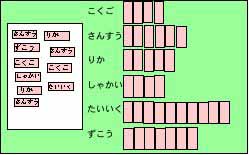
この実践のすごいところは、生徒にとって棒グラフを当たり前のものと考えていないことだろう。そして、グラフの意味と価値も教えているのも素晴らしい。グラフを描けるようにするだけで終わってしまいがちな自分にとっておおいに勉強になった

あけましておめでとう〜年賀パズル

最近は年賀メールが多くなったけどやはり年賀状をこたつでみかんを食べながら一枚一枚読んでいくのは楽しい〜

中でも手作りのもの、版画や絵の年賀状は楽しいね。数学の教員をやっているとそういうのとはちょっと違って数学的な手作り年賀状も頂くことがしばしば、

例えば、

2006=12^3+45×6+7-8+9
2006=（1+2）^3+45×6×7+89
2006=(1-2+3)×4^5+6×7×(8-9)

なんて書きてある(* *) すごい！！！

さらには次のような挑戦状的なものもあった！

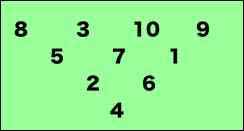
上記は、1〜10までの数を4段の逆ピラミッドに積み上げたもので、上段の二つの数の差（差の絶対値）が下段の数になるようにできているんだそうな。なるほどなるほど、パスカルの三角形の逆バージョンみたいだね。
問題は、「1〜15までの数を同じ数字を2度使わずに5段の逆ピラミッドに同じように積み上げてみよ。」と言うもの。

これを送ってくれたのは若い数学の教員。hideo先生は最近ぼけてるから脳年齢を若くさせるための心遣いかな？ま、何はともあれテレビも下らないのが多いし、暇だったのでちょうど良い時間つぶし...楽しめましたよ。

当たり前のことだけど...

女房は、小学校で教えていて今年は、算数の少人数担当。つまり、算数だけをTT(teem teachingつまり複数教員指導）で教えている。色々な学年、色々なクラスを指導するのでなにかと大変らしい。

TTと言っても担任によって随分と受け止め方に違いがあるらしい。大きな声では言えないが...（書くならいいか？）TTの教員に授業を任せて教室の自分の机で採点作業をしている驚くべき教員がいるらしい。

さすがにウチの女房もあきれて同僚に愚痴ったらしい。そうしたら校長が小耳に挟んだらしく覗きにいったが、ベテラン問題教師は鋭く気配を察知して席を立ったとか。管理職側も粘り強い。今度は教頭が忍び足で再び覗きに来てついに発覚！以後は多少はまともになったとか...なんだかマンガみたいだなぁ〜

こんな先生が1人いるだけで他の人がいい加減と思われるのが腹立たしい！このところ教員バッシングが多い原因もこんなところにあると思う。

そりゃぁ、どんな会社にも問題社員はいるだろう、でも教員はそれと同じに考えることは出来ない。なぜなら仕事の相手は、子ども達であり、直接不満を言えない立場だからだ。また、親は教員・学校を信頼して子どもたちを預けていると言う大前提を忘れてはいけないと思う。

真摯な仕事の姿勢を見せてこそ、子どもや親の信頼も手に出来る。その信頼なしに教育実践なんてできないと思う。

数えることはむずかしい

こうして高校数学を教える立場になった私だが、数列や場合の数の問題をやるときはドキドキする。

例えば、等差数列2,5,8,11,14,....は、２に３を足していくと出来る。だから、n番目は、2+3×n？ いえいえ足した回数はn-1回ですから2+3×(n-1)になる。

こんなこと当たり前ってきっと思っているでしょうね。でも、ぼくはこのn-1が怖いんです。

なぜか？たぶん小学校のときの文章問題で痛い思いをいっぱいしているトラウマなんでしょう。問題の中で果たしてnなのかn-1か、それともn+1かで間違った数々....その度に担任から言われる決まり文句「hideo君、次は落ち着いてもう少し考えてみましょうね」
だから、数える問題が絡むととたんにビビってしまう(^^;)

そんな私に家内から植木算の問題の授業の話。なんでも小学校3年生にそんな単元があるんだそうだ。

問題1　　10本の木を5m間隔で植えたとき端から端まで何mになるか？

例えばこんな問題。何しろ3年生だから5m×10=50mと考えるのは当然だ。しばらく考えさせると5m×(10-1)=45mの意見がでてく来たんだそうだが、その子どもの説明がすごい！

彼は、手のひらをみんなに見せて、「指は5本あるけど指の間は、4個だよ。だから、木は、10本ならその間は、9個。」と言ったのだそうだ。まさに脱帽！　長い間のトラウマが解けてなくなる気分。それにしても、数えるのって難しいね。

問題2　　　50mの道に5m間隔で木を植えたら木は何本になるか？

この問題は、50÷5=10　10+1=11本となり逆に1増えちゃう。さらに、

問題3　　　池の周りに5m間隔に10本の木が植えられているとき、この池の1周の長さは何mになるか？

これだと足すも引くもしないで5m×10=50m

植木算なんて算数の世界だけのことでしょって思われるかもしれないけど、実は色々なところに出てくる。

代表的なところでは、年の問題。平成3年に生まれてた子が平成10年の誕生日には、満7歳。しかし、平成3年に結婚1年目の夫婦は、平成10年には、結婚8年目。オリンピック3連覇した大選手は、8年間世界一の地位にいたことになる。

問題4　　　　2005年から毎年5万円ずつ貯金するとして50万円になるのはいつ？

そんなに難しくない問題だけど、私みたいなうっかり者にはヤバイ問題なんだよね〜

冷蔵庫体育館で...

今日は、部活の大会の引率であった。

最大級の寒波が押し寄せているとか、恐ろしいニュースばかりで昨日から暗い気分でテンションが上がらない...
朝4時半に起きてみると、日の出前の真っ暗な空をひゅーひゅーと風が吹いている「さ...さぶ...さぶい」こんな日に遠征かぁ...

それでも少し気を取り直し、前の日に奥様が買っておいてくれた肉まんと、七味をたっぷり入れたコンソメスープをおなかにしまって外へ出たが。まだ真っ暗...仕事とは分かっているけどやっぱり悲しい気分。

駅から会場までとぼとぼ40分も歩いた...生徒たちも本当に寒そう〜「しっかり歩けばいいウォームアップになるさ」とか言ったけど、気休めとはこのことだね。どうにか会場に着いたが、これがまたすごい体育館で本当に寒い！冷蔵庫の中みたいだ!

試合が始まってよ〜やくテンションが上がって来た。選手は、半袖短パンなので見ているだけで寒そうだが、高校生はやっぱり元気だ。寒い寒いと言いながらよく頑張っていた。負け試合でも最後まで諦めずに食らいついている。こちらも、しらずしらず応援に熱が入る。

試合結果は、1勝3敗で大満足とは言えない、コンディション的にも最悪のつらいつらい1日だったが、帰りの電車に乗ってから生徒たちが晴れ晴れとした表情を見せていたのが印象的だったな。

ハリーポッターブームを振り返る

今晩は、ハリーポッターの映画の新作のを家族みんなで見て来た。実は、ウチの子どもたちはずーっとファンである。

小説「ハリーポッター」は、あんなに厚い本なのに小学生のころから一気に読んでいた。ウチの子だけでなく、僕の生徒の中にも勉強そっちのけで読んでいた不届きものもいたくらいだ。現在は、第一作が書店に並んだときほどの爆発的なブームはないが、それでも映画やDVD でもなかなか人気があるようだ。
　 しかし、なぜこうもこの作品は支持をうけ続けるのか？僕もはじめは魔法や怪物など現実離れしたファンタジーだからウケるのだと思っていたが、どうも違うように思う。

　ハリーポッターの特色（魅力）は、登場人物の生き生きとした心理描写だ。「通常」の児童文学ではあまり出てこない「ねたみ」「さげすみ」「嫌悪感」といった毒々しい人間の心のありようが、主人公も含めてどんどん出てくるし、人間関係でも友人同士の衝突や、周囲からの孤立も頻繁に起こる。これらの「嫌なこと」って子どもの世界では普通なのではないかな。だから若い読者たちから大きな共感を呼ぶのだと思う。

　また、ハリーの家庭環境もなかなか興味深い。ハリーは、ご存知のように両親をウ゛ォルデモート卿に殺され孤児となり、普通の人間の叔父叔母にまったく愛されずに育てられる。11才の誕生日を自分で地面の土に描いたバースデーケーキで祝う場面は今読んでも悲しい。一方で叔父叔母の本当の子どもダドリーは、甘やかされ放題。二人は、一見対照的だ。でも、どちらも扶養者から本当の意味で愛されていないことに変わりはない。このあたりに今の青少年のもつ大人社会全体への不信が読み取れないだろうか。裏を返せば、ハリーを命がけで救い「ウ゛ォルデモート」を愛の力で瀕死にさせた母、守護霊としていつもそばで見守っている父に理想の姿を見たいのだろう。

　そして、最後にもう一つ、主人公ハリーの所属するグリフィンドール寮のスローガンは、「勇気」。まさにそれによってハリーは、絶対悪「ウ゛ォルデモート」と戦い続けることになるが、ここに著者の「子どもたちが逆境にくじけず生きて欲しい」との青少年への熱いメッセージを感じる。

　ハリーがホグワーツ魔法学校を卒業するまでにこれからもハラハラドキドキいろんな出来事が起こるに違いない。それらを一つ一つ乗り越えながら彼は一歩また一歩成長していくのが楽しみだ。しかし、多くの若い読者たちもまた、ハリーおなじような体験をしているんじゃないだろうか？その親近感こそがハリーポッターの面白さのように思う。

平面図形の世界を体験する、分かる、広げる(後段）

[F]円に内接する四角形と三角比を組み合わせる
　三角比を習うまでに平面図形領域が終わっていれば、三角比の正弦定理、余弦定理、面積公式などを用いれば様々な授業展開の可能性が広がる。

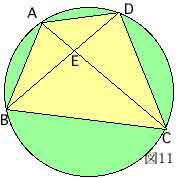
　例えば、図11でAE,BE,CEの長さと∠BEAが分かっていれば、方べきの定理によりDEを求めることができる。

さらに、
面積公式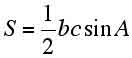より
(f) 対角線で区切られた三角形や四角形ABCDの面積が求まる。
また、余弦定理より
(g) 四角形ABCDの４辺の長さを求めることができる。

　では、4辺の長さが与えられたらどうか？
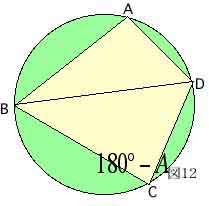(図12）

∠BAD=∠A,∠BCD=∠Cとして、△ABD、△CBDに余弦定理を用いれば、

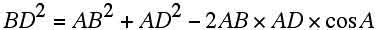.....(ウ)
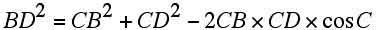.....(エ)

「円に内接する四角形の対角の和は180°」の性質を三角比を活用すると

(h) sin A=sinC cosA= -cosC だから(エ)の式は、

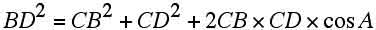......(オ)

(ウ)(オ)からcosAを消去すれば、
(i) 対角線BDの長さ を求めることができる。

また、(ウ)(オ)からBDを消去すれば、
(j) cosA が求まるから、
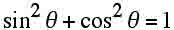により
(k) sinA が求まる。

そこで面積公式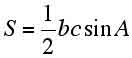 を用いれば、
(l)△ABD,△CDBの面積 , 四角形ABCDの面積を求めることができる。

△ABDに正弦定理 を用いれば、
(m)四角形ABCDの内接する円の半径R を求めることができる。

その他、次の値も求めることも可能である。
(n) 図4で、AE,BE,CE,DEの長さ
(o) sin∠BACなど辺と対角線なす角の正弦
(p) cos∠ABEなど２本の対角線のなす角の余弦
(q) 対角線で区切られた4つの三角形の面積
　以上のことから円に内接する四角形では、４辺の長さえ分かれば、図11にあらわれる図形的な値のほとんどを計算出来ることが分かる。

[G]トレミーの定理から加法定理を証明する

　トレミーの定理による加法定理の証明は明快であり、歴史的にも由緒正しい方法でもあると思う。以下の証明は、アルマゲストの著述とは少し違うが授業では分かり易いだろう。

　まず、直径1の円に内接し、対角線の1本が直径となる四角形を用意する。
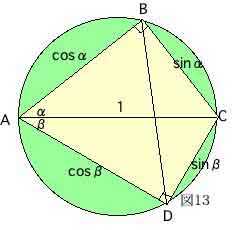（図13）

AB=cosα、BC=sinα
AD=cosβ、CD=sinβ
はあきらか、

△ABDに正弦定理をもちいると
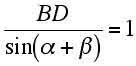だからBD=sin(α+β）が分かる。

ここでトレミーの定理を用いると
1×sin(α+β）=cosα×sinβ+sinα×cosβ
よって
(r) sin(α+β）=sinα・cosβ+cosα・sinβ
(証明終わり)

[H]三角表の完成へ
　現在の指導要領の三角比・三角関数は30°45°60°などの角度がほとんどで三角表を活用する場面が少ない。三角表を古代の人がどうやって作ったかを学ぶことで、三角表の意義を理解できるだろう。
　加法定理から半角の公式を導けば、15°、7.5°あるいは、22.5°の三角比を求めることは容易である
　トレミーは、72°の三角比からさらに細かい角度の三角比を求めているが、ここでは、正五角形を用いた36°の三角比を求め方を紹介する。

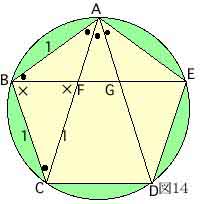
　図14は、一辺の長さが1の正五角形である。

正五角形の内角は、108°だから∠BAC=108°÷3=36°

　ここで、対角線ACの長さを*とすると、
△ABF∽△ACB だからAB:AC=AF:ABより
1：x=(x-1):1
　
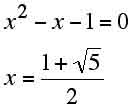
△ABCに余弦定理を用いて

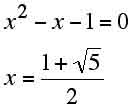
36°-30°=6°だから加法定理を用いて、6°の三角比を求めることができる。ここに半角の公式を用いれば、3°さらには、1.5°の三角比も求めることができる。

【4】平面図形領域の可能性
　平面図形領域は、現在の教員の大半が高校時代に教わっておらず幾分かの苦手意識の中で指導しているように思う。一方、数学Aの教科書には昔ながらの初等幾何を思わせる記述が多い。
　しかし、平面図形領域は他領域へのダイナミックなアプローチになることはトレミーの定理・加法定理の関係を見れば明らかである。また、平面図形領域の指導法は、円に内接する四角形と平行四辺形の関係の対称性を見れば、まだまだ工夫できそうだ。　　現場の教員それぞれが、過去の初等幾何の遺産を受け継ぐ一方で、過去に捉われず、新たな研究・工夫をすることで平面図形は微分積分に負けない高校数学の主役になれるように思う。

参考文献　
オリガミクス　芳賀和夫著　日本評論社刊
アルマゲスト　薮内　清訳　恒星社刊

平面図形の世界を体験する、分かる、広げる(中段）

すみません当初の方針を変えて3部に分けて掲載します。

【3】平面図形領域の教材を再検討する
　平面図形領域の教材は、研究の余地はないのだろうか？他領域との関係も踏まえながら再検討する。

[D]四角形の分類を見直す
　四角形の分類と言えば、（図4）のように台形-平行四辺形-長方形（ひし形）-正方形と形状で分類されるのが普通だ。

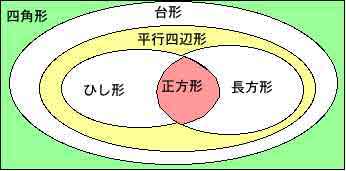
*図4
しかし、高校では（図5）のように平行四辺形と円に内接する四角形に分けるのが良いと思う。

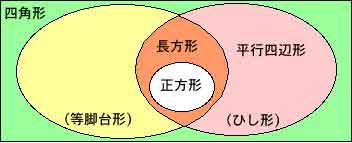
*図5
　図形の形状からは、この２つの四角形が相対するものだとは思いにくいが、平行四辺形が「隣り合う角の和は180°」なのに対し、円に内接する四角形は、「向かい合う角の和は180°」となり実は対称的な性質をもつ。また、この２つの四角形の共通部分は長方形になるというのも意味が重い。

[E]平行四辺形と円に内接する四角形の対称性

(1)方べきの定理
　円に内接する四角形では、方べきの定理
(a) AE×CE=BE×DE がなりたつ。

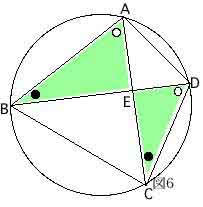
証明は、図6のように円周角の定理から△AEB∽△DECとなりその相似比からできる

　一方、平行四辺形では、
　
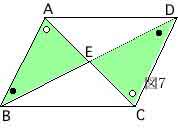
図7のように錯角の性質と向い合う辺の長さが等しいことから△AEB≡△CEDなので
(b) AE=CEかつBE=DE

　ここで四角形ABCDが円に内接し平行四辺形でもあるとすれば、(a)(b)両方から「AE=BE=CE=DE」になるが、これは、長方形の性質である。

(2)トレミー（プトレマイオス）の定理
　円に内接する四角形の辺と対角線の長さについて
(c) AC・BD=AB・CD+BC・AD がなりたつ。
これをトレミー（プトレマイオス）の定理という。

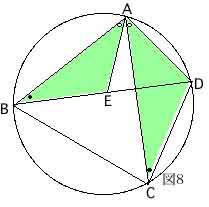
　トレミーは、アレキサンドリアでAD127〜151に活躍した天文学者で、天動説による天体の運動理論を完成させた。この定理は、著書アルマゲストに載っていて、この定理を使うことで三角比の加法定理を導き、天文計算に不可欠な三角表を完成に導いている。

　証明するには、図8のように補助線AEを引く。

△ABE∽△ADCだからAB:AC=BE:CDすなわち
AB・CD=AC・BE.....(ア)

また、∠BAC=∠EAD、∠ACB=∠ADEだから
△ABC∽△AEDとなりBC:ED=AC:ADすなわち
BC・AD=AC・ED.....(イ)

(ア)と（イ）を左辺どうし、右辺どうし加えると
AB・CD+BC・AD=AC・BE+AC・ED
AB・CD+BC・AD=AC・BD
（証明終わり）

　特殊な補助線を引かねばならない点は問題だが、相似比だけで証明できる。チェバの定理の証明と比べても難しくはないだろう。

　トレミーの定理のように四角形の辺の長さと対角線の性質を平行四辺形で探すと、

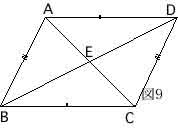
(d)AB=CD , BC=AD （図9）がある。

　ここで四角形ABCDが、円に内接する四角形と平行四辺形のの両方の性質をもつとすれば、性質(c)と(d)の両方を満たすから、
(e) 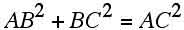となる。

　これは、ピタゴラスの定理である。

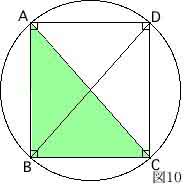
このことから、ピタゴラスの定理は、直角三角形ではなく長方形の辺と対角線に成り立つ性質との見方をしてもよいだろう。
　平行四辺形は、ベクトル等でも扱われることが多いが、円に内接する四角形は他領域の学習ではあまり扱われてこなかった。しかし、平行四辺形と相対する性質をもつと思われるので、円に内接する四角形は、もっと積極的に学ばせた方が良いだろう。

平面図形の世界を体験する、分かる、広げる(前段）

今年の研究会での論文です。これまでの記事と多少重複しますが3回に分けて掲載します。

【1】高校生に平面図形を教える問題点を整理する
　これまでの経験から、高校生に平面図形を教えるにあたっての問題点を次の４つと考えている。
(1)図形の概念へのリアルなイメージがない
　例えば、△ABCにおいて、角Aの二等分線、点Aと辺BC中点を結ぶ線分（中線）、辺BCの垂直二等分線、どれも三角形を２つに分ける線と言える。しかし、この３本の区別があやふやな生徒が多い。このように図形的な思考のイメージが不足しているのは、子供時代からの図形体験が乏しいのではないからだろうか。

(2)図形の定理の証明に苦手意識をもっている　　平面図形の理解の浅い生徒が定理の証明の繰り返しで平面図形を理解するのは適無理があると思われる。証明に苦手意識をもつ生徒は、自分がうまく証明が理解できないことと平面図形の性質が分からないことを混同してしまうようだ。

(3)問題を解くのに直感が必要となる。
　生徒は決まった方法（パターン）で解答できる問題を好む。教員もそうした方向に授業展開を考えがちだ。逆に、直感がないと答えが見つからない問題は、さけられることが多い。平面図形領域ではそうした直感の壁を超えねばならない場面が多い。

(4)中学での学習が定着していない生徒が多い
　基本事項も理解できていない生徒は多い。平面図形領域の学習では、論理的に理解することが繰り返されるので、分からないこと1つがその後の学習の流れを止め、意欲を削ぐことになりがちである。

【2】問題点を解決するには
　 【1】で述べた問題点に配慮した具体的な授業方法について提案する。

[A]コンパスと定規を使う前に折り紙で導入　
　コンパスも定規も苦手な生徒がいるので、まず折り紙で図形的なイメージを手を使って活動させる。

(1)三角形の色紙を用意する。その三角形の一辺の垂直二等分線を折らせる。折り方を確認したら残りの辺でも折らせる。時間の余裕があれば中線や角の二等分線でも試させるのもよい*
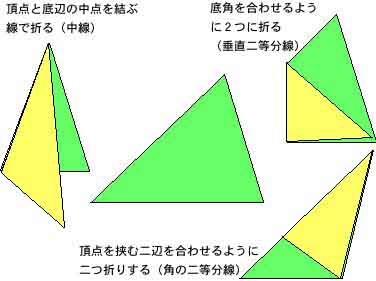図1
　　　　※外心は中学で未習
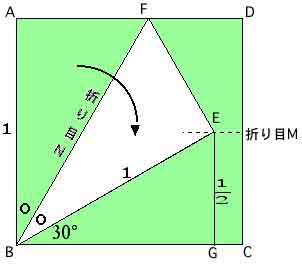
(2)折り紙を用意する。それを使って45°を折らせる。次に60°を折らせる。
（1：2になる直角三角形を作れば良いとヒントを出す）　参照：オリガミクス　芳賀和夫著　日本評論社刊
*図2

[B]中学の平面図形領域を復習する。　
　平面図形領域に関しては、苦手意識を持ち未習得な生徒が多い。また、作図体験も少ないようだ。そこで3時間で作図を中心に中学の範囲を復習する。

(1)作図の基礎
線分を1辺とする正三角形
1点から線分への垂線
線分の垂直二等分線
角の二等分線
線分を1辺とする正方形
線分を1辺とする正六角形
(2)合同な図形/平行四辺形
三角形の合同条件
合同な三角形の作図
平行四辺形の成立条件
平行四辺形の作図
同位角・錯角の性質（問題演習）
(3)相似な図形/円周角の定理
三角形の相似条件
相似比の性質（問題演習）
円周角と中心角の性質
円に内接する四角形の角度（問題演習）

[C]作業と思考が両立した授業展開をする　
　平面図形領域では、図形作業で性質を発見する活動（体感的理解）と論理的な思考で性質を証明する活動（思考的理解）の両方が満たされて初めて本当の理解（心理的理解）が達成されるように思う。

　今の生徒たちは、図形体験が乏しくリアルなイメージが湧かないので、かつての初等幾何の授業ではうまくいかない。そこで、論理的証明に加えて、作図などの作業も積極的に行わせたい。また、作業がうまくできたという成功体験が、図形への苦手意識を克服させるように思う。

　作図をした後に長さや角度の計測もすることで一段と図形の性質を実感できるように思う。さらに、計測した数値から規則性を発見できるようにすれば、図形の性質への気づき（ひらめき）が面白いと感じられるきっかけになるだろう。
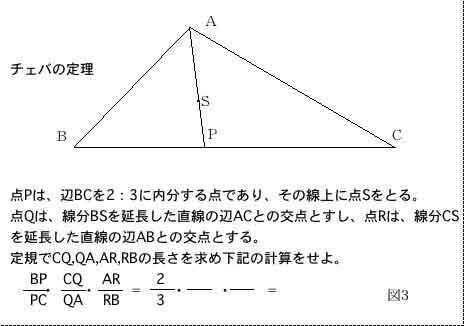
　例えば、難しいチェバの定理もプリント（図3）で作図をさせた後で計らせて、数人の生徒の結果を板書しそれの平均値をとったところ0.98〜1.02の範囲になり定理の正確さを証明する前に「本当らしい」と納得することができた。そのあと少々難しい証明を示しても前向きに学習できたように思う。

　作業と思考を次のような流れで組み合わせる授業が理想的だろう。
❶作図作業（まずやってみよう）
　　⇩
❷図形の共通性質の探究（どうなってるの？）
　　⇩
❸性質の発見（こうなっているらしい）
　　⇩
❹証明への渇望（ほんとうかな？）
　　⇩
❺証明の達成（なっとく！）

全ての教材でこの流れにするのは難しいが、方べきの定理、メネラウスの定理、外心作図法の探求などではかなり効果的だ。