平面図形の世界を体験する、分かる、広げる(中段）

すみません当初の方針を変えて3部に分けて掲載します。

【3】平面図形領域の教材を再検討する
　平面図形領域の教材は、研究の余地はないのだろうか？他領域との関係も踏まえながら再検討する。

[D]四角形の分類を見直す
　四角形の分類と言えば、（図4）のように台形-平行四辺形-長方形（ひし形）-正方形と形状で分類されるのが普通だ。

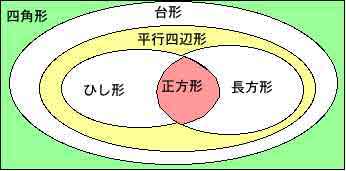
*図4
しかし、高校では（図5）のように平行四辺形と円に内接する四角形に分けるのが良いと思う。

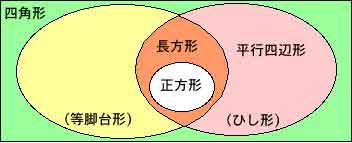
*図5
　図形の形状からは、この２つの四角形が相対するものだとは思いにくいが、平行四辺形が「隣り合う角の和は180°」なのに対し、円に内接する四角形は、「向かい合う角の和は180°」となり実は対称的な性質をもつ。また、この２つの四角形の共通部分は長方形になるというのも意味が重い。

[E]平行四辺形と円に内接する四角形の対称性

(1)方べきの定理
　円に内接する四角形では、方べきの定理
(a) AE×CE=BE×DE がなりたつ。

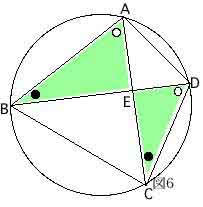
証明は、図6のように円周角の定理から△AEB∽△DECとなりその相似比からできる

　一方、平行四辺形では、
　
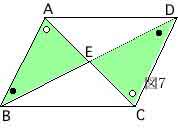
図7のように錯角の性質と向い合う辺の長さが等しいことから△AEB≡△CEDなので
(b) AE=CEかつBE=DE

　ここで四角形ABCDが円に内接し平行四辺形でもあるとすれば、(a)(b)両方から「AE=BE=CE=DE」になるが、これは、長方形の性質である。

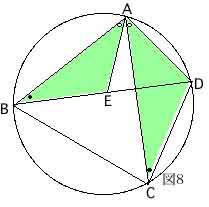
(2)トレミー（プトレマイオス）の定理
　円に内接する四角形の辺と対角線の長さについて
(c) AC・BD=AB・CD+BC・AD がなりたつ。
これをトレミー（プトレマイオス）の定理という。

　トレミーは、アレキサンドリアでAD127〜151に活躍した天文学者で、天動説による天体の運動理論を完成させた。この定理は、著書アルマゲストに載っていて、この定理を使うことで三角比の加法定理を導き、天文計算に不可欠な三角表を完成に導いている。

　証明するには、図8のように補助線AEを引く。

△ABE∽△ADCだからAB:AC=BE:CDすなわち
AB・CD=AC・BE.....(ア)

また、∠BAC=∠EAD、∠ACB=∠ADEだから
△ABC∽△AEDとなりBC:ED=AC:ADすなわち
BC・AD=AC・ED.....(イ)

(ア)と（イ）を左辺どうし、右辺どうし加えると
AB・CD+BC・AD=AC・BE+AC・ED
AB・CD+BC・AD=AC・BD
（証明終わり）

　特殊な補助線を引かねばならない点は問題だが、相似比だけで証明できる。チェバの定理の証明と比べても難しくはないだろう。

　トレミーの定理のように四角形の辺の長さと対角線の性質を平行四辺形で探すと、

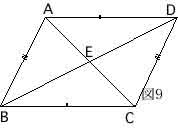
(d)AB=CD , BC=AD （図9）がある。

　ここで四角形ABCDが、円に内接する四角形と平行四辺形のの両方の性質をもつとすれば、性質(c)と(d)の両方を満たすから、
(e) 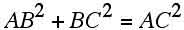となる。

　これは、ピタゴラスの定理である。

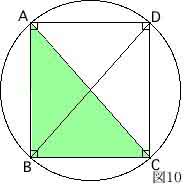
このことから、ピタゴラスの定理は、直角三角形ではなく長方形の辺と対角線に成り立つ性質との見方をしてもよいだろう。
　平行四辺形は、ベクトル等でも扱われることが多いが、円に内接する四角形は他領域の学習ではあまり扱われてこなかった。しかし、平行四辺形と相対する性質をもつと思われるので、円に内接する四角形は、もっと積極的に学ばせた方が良いだろう。