平面図形の世界を体験する、分かる、広げる(後段） [研究会で]
[F]円に内接する四角形と三角比を組み合わせる
三角比を習うまでに平面図形領域が終わっていれば、三角比の正弦定理、余弦定理、面積公式などを用いれば様々な授業展開の可能性が広がる。
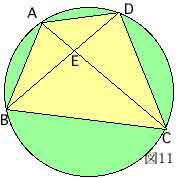
例えば、図11でAE,BE,CEの長さと∠BEAが分かっていれば、方べきの定理によりDEを求めることができる。
さらに、
面積公式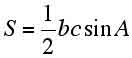
より
(f) 対角線で区切られた三角形や四角形ABCDの面積が求まる。
また、余弦定理より
(g) 四角形ABCDの４辺の長さを求めることができる。
では、4辺の長さが与えられたらどうか？
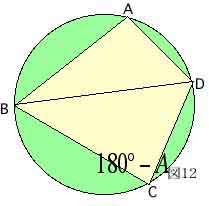(図12）
∠BAD=∠A,∠BCD=∠Cとして、△ABD、△CBDに余弦定理を用いれば、
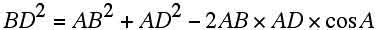.....(ウ)
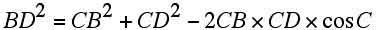.....(エ)
「円に内接する四角形の対角の和は180°」の性質を三角比を活用すると
(h) sin A=sinC cosA= -cosC だから(エ)の式は、
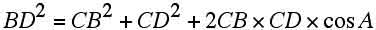......(オ)
(ウ)(オ)からcosAを消去すれば、
(i) 対角線BDの長さ を求めることができる。
また、(ウ)(オ)からBDを消去すれば、
(j) cosA が求まるから、
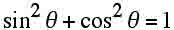により
(k) sinA が求まる。
そこで面積公式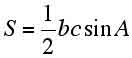 を用いれば、
(l)△ABD,△CDBの面積 , 四角形ABCDの面積を求めることができる。
△ABDに正弦定理 を用いれば、
(m)四角形ABCDの内接する円の半径R を求めることができる。
その他、次の値も求めることも可能である。
(n) 図4で、AE,BE,CE,DEの長さ
(o) sin∠BACなど辺と対角線なす角の正弦
(p) cos∠ABEなど２本の対角線のなす角の余弦
(q) 対角線で区切られた4つの三角形の面積
以上のことから円に内接する四角形では、４辺の長さえ分かれば、図11にあらわれる図形的な値のほとんどを計算出来ることが分かる。
[G]トレミーの定理から加法定理を証明する
トレミーの定理による加法定理の証明は明快であり、歴史的にも由緒正しい方法でもあると思う。以下の証明は、アルマゲストの著述とは少し違うが授業では分かり易いだろう。
まず、直径1の円に内接し、対角線の1本が直径となる四角形を用意する。
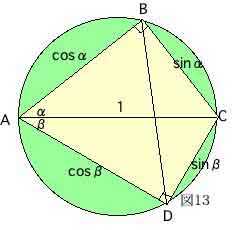（図13）
AB=cosα、BC=sinα
AD=cosβ、CD=sinβ
はあきらか、
△ABDに正弦定理をもちいると
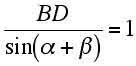だからBD=sin(α+β）が分かる。
ここでトレミーの定理を用いると
1×sin(α+β）=cosα×sinβ+sinα×cosβ
よって
(r) sin(α+β）=sinα・cosβ+cosα・sinβ
(証明終わり)
[H]三角表の完成へ
現在の指導要領の三角比・三角関数は30°45°60°などの角度がほとんどで三角表を活用する場面が少ない。三角表を古代の人がどうやって作ったかを学ぶことで、三角表の意義を理解できるだろう。
加法定理から半角の公式を導けば、15°、7.5°あるいは、22.5°の三角比を求めることは容易である
トレミーは、72°の三角比からさらに細かい角度の三角比を求めているが、ここでは、正五角形を用いた36°の三角比を求め方を紹介する。
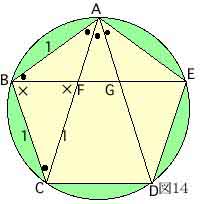
図14は、一辺の長さが1の正五角形である。
正五角形の内角は、108°だから∠BAC=108°÷3=36°
ここで、対角線ACの長さを*とすると、
△ABF∽△ACB だからAB:AC=AF:ABより
1：x=(x-1):1
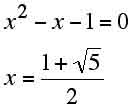
△ABCに余弦定理を用いて
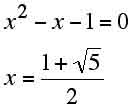
36°-30°=6°だから加法定理を用いて、6°の三角比を求めることができる。ここに半角の公式を用いれば、3°さらには、1.5°の三角比も求めることができる。
【4】平面図形領域の可能性
平面図形領域は、現在の教員の大半が高校時代に教わっておらず幾分かの苦手意識の中で指導しているように思う。一方、数学Aの教科書には昔ながらの初等幾何を思わせる記述が多い。
しかし、平面図形領域は他領域へのダイナミックなアプローチになることはトレミーの定理・加法定理の関係を見れば明らかである。また、平面図形領域の指導法は、円に内接する四角形と平行四辺形の関係の対称性を見れば、まだまだ工夫できそうだ。 現場の教員それぞれが、過去の初等幾何の遺産を受け継ぐ一方で、過去に捉われず、新たな研究・工夫をすることで平面図形は微分積分に負けない高校数学の主役になれるように思う。
参考文献
オリガミクス 芳賀和夫著 日本評論社刊
アルマゲスト 薮内 清訳 恒星社刊
平面図形の世界を体験する、分かる、広げる(中段） [研究会で]
すみません当初の方針を変えて3部に分けて掲載します。
【3】平面図形領域の教材を再検討する
平面図形領域の教材は、研究の余地はないのだろうか？他領域との関係も踏まえながら再検討する。
[D]四角形の分類を見直す
四角形の分類と言えば、（図4）のように台形-平行四辺形-長方形（ひし形）-正方形と形状で分類されるのが普通だ。
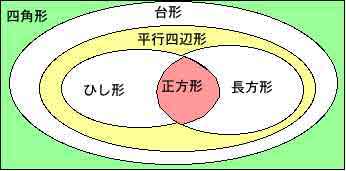
*図4
しかし、高校では（図5）のように平行四辺形と円に内接する四角形に分けるのが良いと思う。
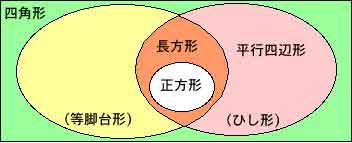
*図5
図形の形状からは、この２つの四角形が相対するものだとは思いにくいが、平行四辺形が「隣り合う角の和は180°」なのに対し、円に内接する四角形は、「向かい合う角の和は180°」となり実は対称的な性質をもつ。また、この２つの四角形の共通部分は長方形になるというのも意味が重い。
[E]平行四辺形と円に内接する四角形の対称性
(1)方べきの定理
円に内接する四角形では、方べきの定理
(a) AE×CE=BE×DE がなりたつ。
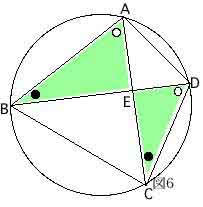
証明は、図6のように円周角の定理から△AEB∽△DECとなりその相似比からできる
一方、平行四辺形では、
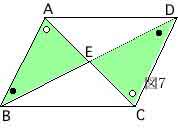
図7のように錯角の性質と向い合う辺の長さが等しいことから△AEB≡△CEDなので
(b) AE=CEかつBE=DE
ここで四角形ABCDが円に内接し平行四辺形でもあるとすれば、(a)(b)両方から「AE=BE=CE=DE」になるが、これは、長方形の性質である。
(2)トレミー（プトレマイオス）の定理
円に内接する四角形の辺と対角線の長さについて
(c) AC・BD=AB・CD+BC・AD がなりたつ。
これをトレミー（プトレマイオス）の定理という。
トレミーは、アレキサンドリアでAD127〜151に活躍した天文学者で、天動説による天体の運動理論を完成させた。この定理は、著書アルマゲストに載っていて、この定理を使うことで三角比の加法定理を導き、天文計算に不可欠な三角表を完成に導いている。
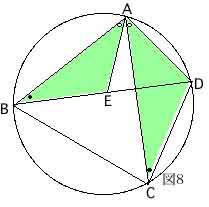
証明するには、図8のように補助線AEを引く。
△ABE∽△ADCだからAB:AC=BE:CDすなわち
AB・CD=AC・BE.....(ア)
また、∠BAC=∠EAD、∠ACB=∠ADEだから
△ABC∽△AEDとなりBC:ED=AC:ADすなわち
BC・AD=AC・ED.....(イ)
(ア)と（イ）を左辺どうし、右辺どうし加えると
AB・CD+BC・AD=AC・BE+AC・ED
AB・CD+BC・AD=AC・BD
（証明終わり）
特殊な補助線を引かねばならない点は問題だが、相似比だけで証明できる。チェバの定理の証明と比べても難しくはないだろう。
トレミーの定理のように四角形の辺の長さと対角線の性質を平行四辺形で探すと、
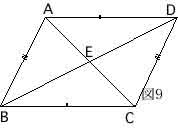
(d)AB=CD , BC=AD （図9）がある。
ここで四角形ABCDが、円に内接する四角形と平行四辺形のの両方の性質をもつとすれば、性質(c)と(d)の両方を満たすから、
(e)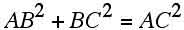 
となる。
これは、ピタゴラスの定理である。
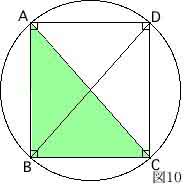
このことから、ピタゴラスの定理は、直角三角形ではなく長方形の辺と対角線に成り立つ性質との見方をしてもよいだろう。
平行四辺形は、ベクトル等でも扱われることが多いが、円に内接する四角形は他領域の学習ではあまり扱われてこなかった。しかし、平行四辺形と相対する性質をもつと思われるので、円に内接する四角形は、もっと積極的に学ばせた方が良いだろう。
平面図形の世界を体験する、分かる、広げる(前段） [研究会で]
今年の研究会での論文です。これまでの記事と多少重複しますが3回に分けて掲載します。
【1】高校生に平面図形を教える問題点を整理する
これまでの経験から、高校生に平面図形を教えるにあたっての問題点を次の４つと考えている。
(1)図形の概念へのリアルなイメージがない
例えば、△ABCにおいて、角Aの二等分線、点Aと辺BC中点を結ぶ線分（中線）、辺BCの垂直二等分線、どれも三角形を２つに分ける線と言える。しかし、この３本の区別があやふやな生徒が多い。このように図形的な思考のイメージが不足しているのは、子供時代からの図形体験が乏しいのではないからだろうか。
(2)図形の定理の証明に苦手意識をもっている 平面図形の理解の浅い生徒が定理の証明の繰り返しで平面図形を理解するのは適無理があると思われる。証明に苦手意識をもつ生徒は、自分がうまく証明が理解できないことと平面図形の性質が分からないことを混同してしまうようだ。
(3)問題を解くのに直感が必要となる。
生徒は決まった方法（パターン）で解答できる問題を好む。教員もそうした方向に授業展開を考えがちだ。逆に、直感がないと答えが見つからない問題は、さけられることが多い。平面図形領域ではそうした直感の壁を超えねばならない場面が多い。
(4)中学での学習が定着していない生徒が多い
基本事項も理解できていない生徒は多い。平面図形領域の学習では、論理的に理解することが繰り返されるので、分からないこと1つがその後の学習の流れを止め、意欲を削ぐことになりがちである。
【2】問題点を解決するには
【1】で述べた問題点に配慮した具体的な授業方法について提案する。
[A]コンパスと定規を使う前に折り紙で導入
コンパスも定規も苦手な生徒がいるので、まず折り紙で図形的なイメージを手を使って活動させる。
(1)三角形の色紙を用意する。その三角形の一辺の垂直二等分線を折らせる。折り方を確認したら残りの辺でも折らせる。時間の余裕があれば中線や角の二等分線でも試させるのもよい*
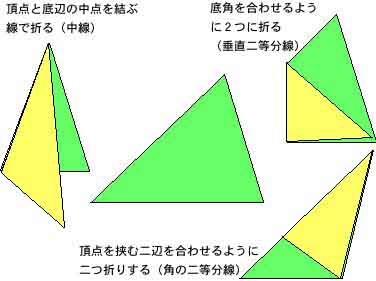図1
※外心は中学で未習
(2)折り紙を用意する。それを使って45°を折らせる。次に60°を折らせる。
（1：2になる直角三角形を作れば良いとヒントを出す） 参照：オリガミクス 芳賀和夫著 日本評論社刊
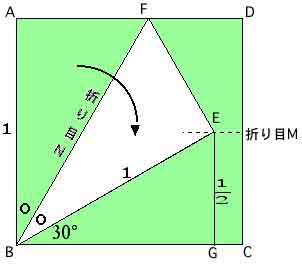*図2
[B]中学の平面図形領域を復習する。
平面図形領域に関しては、苦手意識を持ち未習得な生徒が多い。また、作図体験も少ないようだ。そこで3時間で作図を中心に中学の範囲を復習する。
(1)作図の基礎
線分を1辺とする正三角形
1点から線分への垂線
線分の垂直二等分線
角の二等分線
線分を1辺とする正方形
線分を1辺とする正六角形
(2)合同な図形/平行四辺形
三角形の合同条件
合同な三角形の作図
平行四辺形の成立条件
平行四辺形の作図
同位角・錯角の性質（問題演習）
(3)相似な図形/円周角の定理
三角形の相似条件
相似比の性質（問題演習）
円周角と中心角の性質
円に内接する四角形の角度（問題演習）
[C]作業と思考が両立した授業展開をする
平面図形領域では、図形作業で性質を発見する活動（体感的理解）と論理的な思考で性質を証明する活動（思考的理解）の両方が満たされて初めて本当の理解（心理的理解）が達成されるように思う。
今の生徒たちは、図形体験が乏しくリアルなイメージが湧かないので、かつての初等幾何の授業ではうまくいかない。そこで、論理的証明に加えて、作図などの作業も積極的に行わせたい。また、作業がうまくできたという成功体験が、図形への苦手意識を克服させるように思う。
作図をした後に長さや角度の計測もすることで一段と図形の性質を実感できるように思う。さらに、計測した数値から規則性を発見できるようにすれば、図形の性質への気づき（ひらめき）が面白いと感じられるきっかけになるだろう。
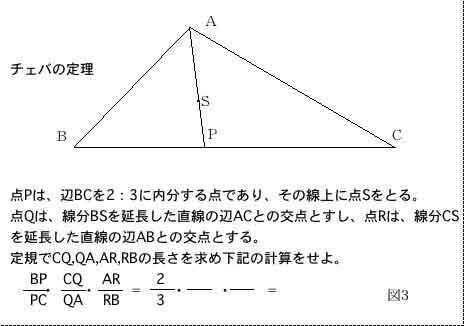
例えば、難しいチェバの定理もプリント（図3）で作図をさせた後で計らせて、数人の生徒の結果を板書しそれの平均値をとったところ0.98〜1.02の範囲になり定理の正確さを証明する前に「本当らしい」と納得することができた。そのあと少々難しい証明を示しても前向きに学習できたように思う。
作業と思考を次のような流れで組み合わせる授業が理想的だろう。
❶作図作業（まずやってみよう）
⇩
❷図形の共通性質の探究（どうなってるの？）
⇩
❸性質の発見（こうなっているらしい）
⇩
❹証明への渇望（ほんとうかな？）
⇩
❺証明の達成（なっとく！）
全ての教材でこの流れにするのは難しいが、方べきの定理、メネラウスの定理、外心作図法の探求などではかなり効果的だ。
11月の研究会 [研究会で]
久しぶりの研究会！ここのところ中々忙しく数学の勉強もできずにいたので良いリフレッシュになった。
私のもっかの研究テーマは、数学Aの平面図形領域つまり初等幾何の他の数学への活用。以前、円に内接する四角形と平行四辺形の関係の記事を書いたがそれもその一連の話。
今回は、古代ギリシャの学者ヒッパルコスとトレミーらが三角表をどうやって作ったか？
正三角形と直角二等辺三角形を用いれば、30°、45°、60°の三角比は、求められる。また、トレミーの定理により三角比の加法定理が証明されるので、15°、75°も求められる。ここまでは簡単。
次に登場するのが正五角形
1辺の長さを1とするとき、対角線ACの長さxを求めることにする。細かい説明は省くが、∠BAC=∠CAD=∠DAEだから∠BAC=1/3×∠BAE=1/3×108°=36°
また、AB=BC=CF=1 だから、AF=x-1
△ABF∽△ACB （どちらも36°の底角の２等辺三角形）だから、
AB:AF=AC:AB つまり 1：x-1=x：1
△ABCの三辺の長さが求まったので余弦定理を∠BACに用いて
これにより36°の三角比が求まるから加法定理より36°-30°=6°で6°の三角比が求まる。ここに半分角の定理を用いれば、3°、さらに1.5°、0.75°の三角比が求まる。
そこから先は、研究会でT先生から教えて頂いた。1°の三角比は幾何的には求まらないので、計算術を駆使して近似値を追求していったとのこと2000年以上前にそんなことをやっていた彼らの頭脳には脱帽するしかない。
薮内清先生の訳されたアルマゲストを開くと、6°、3°、1.5°、0.75°の三角比を見つけていった経緯が詳しく書いてある。本を通して2000年の向こうから手紙をもらった気分でなんか嬉しい(^^)
10月の研究会 [研究会で]
僕からの報告は、ブログでも紹介して来たこと
四角形の分類と言えば、台形→平行四辺形→長方形→正方形とするが、高校では、平行四辺形と円に内接する四角形に分けるのはどうかとの提案。
同席した教員の間でも平行四辺形と円に内接する四角形の共通部分は、長方形になるということは新鮮だったようだ。新課程で数学Aに初等幾何が入って来てからはや３年。平面図形の性質をもっと利用した授業の展開を考えていきたい。特に円に内接する四角形に関する部分は、積極的に取り上げたい。
インターネットで検索をしたりして調べてみたが、
問題1 次の図のxを求めよ。
問題2 次の等脚台形の下底の長さを求めよ。
上記の2問なんかはそれほど難しくなく実際の授業で使えそうだ。
他の研究員の方からも、まだまだ具体化が足りないとの指摘もあった。２月の発表会にむけてもう少し考えていきたい。
9月25日 学力低下問題の真実 [研究会で]
研究会で、今年度当初からマスコミで話題の学力低下問題について講演会を行う事にしました。
講師は、教育報道出版社の梶浦真さん。学力問題についてとても詳しい方なんです。少し長いけど報告します。
梶浦さんが、まず語ったのは、2003年のPISAの学力検査で日本の順位が下がったことが話題になっているが、2000年と2003年では出題の仕方が変わっていて、2000年と2003年の同じタイプの出題分野では日本の順位は依然として大変高いことでした。
そして、2003年の順位が下がった事を総合的な学習の時間を始めとする新学習指導要領に原因とする説は科学的に根拠が無いとの指摘には驚かされました。
氏によれば、学ぶ事は、 A-トレーニング（ドリル的学習） B-ラーニング（受動的な学習） C-スタディ（主体的な学び）の三段階があり、そのどれもが必要であり、マスコミによる「総合的な学習の時間」対「教科学習」のような二者択一的思考は、間違いとのこと。
学力を高めたいのなら、学習の時間や手段を厳しくする事だけではなく、生徒たちが関わり合いながら学び、理解を共有しながら、お互いを磨き合う学習形態に変えていくべきでだそうです。
こうした方法は、ともすると理想の空論と思われがちですが、教育学での調査で、共同学習は、競争学習や個別学習の方法より成果が上がる事が報告されているそうです。
アメリカでは、新しい時代に向けた教育改革の計画が現在進んでおりそのポイントは、次の3つです。
（1）現在の学習方法の多くは、工業化社会の中で作られたもので、与えられた課題をこなすのが上手な人間を育成するものである
（2）一般大衆は、暗記することを学習と考えている
（3）協同的に課題を解決する力を伸ばし、未熟であっても持てる力を応用し解決する力をつけるカリキュラムが今後は必要である
う〜ん、今まで聞いていた話と違いすぎて、ともかく驚きました。そして、深く考えさせられる講演でした。
参考図書
学力低下より怖い！ 「学欲低下」 梶浦真（教育報道出版社）
恊働学力〜知の創造とこれからの学び〜 梶浦真（教育報道出版社）
8月27日 対数へのネイピアの情熱 [研究会で]
夏の数学の研修会で、湘南工科大学の桜井進先生の講演を拝聴する事が出来ました。
題目は、「ジョン・ネイピア対数誕生物語」でしたが、コンピュータとi podをプロジェクターとアンプ+スピーカーにをつないで映像と音楽をふんだんに利用した素晴らしい講演で、驚くとともに最後まで興味深く学ぶ事ができました。
対数を最初に考えたのがジョン・ネイピア（1550〜1617）であることは良く知られた事実ですが、対数が指数より先に考えられた事は余り知られていません。僕も何年か前に初めて知りました。
今回の講演で何故ネイピアが対数を考えるに至ったかを初めて知り大変驚きました。
当時は、大航海時代のために地図上の正確な位置を天体観測でより正確に求める必要が合ったのですが、その計算はまさに天文学的数値の計算のため困難を極めました。そのため、不十分な計算値による航行を強いられ船の難破しばしば起こっていたそうです。
まず、驚いたのがネイピアが地方の城主であって数学者でなかったと言う事です。では、なぜ数学の研究を行ったのか？ 海難事故を減らすためには新しい計算方法を開発しなければいけないとの使命感からだったそうです。スコットランドでは、今でも彼の業績を高く讃えているとのこと。数学の研究者ではまことに珍しい話です。
もう一つ面白かったのが、限られた時間で対数表を完成をするために、全ての桁の計算をすることを捨てた決断。
81226703×59478362=4831231245100486 と計算するのではとてもじゃないが膨大な時間が必要になってしまうので
81226703×59478362=4.83123×10の15乗 と言う答えで済ますという妥協をしたのだそうです。自分の研究が自分の死で挫折する事を恐れたからだとか...なかなか凄い話ですね。
ネイピアの真実を少しでも知る事が出来て本当に良かった。(^o^)
6月26日 平面図形の導入 [研究会で]
先日の研究会で以前に発表した事のある平面図形の導入の話をしました。最近の中学では、僕らの時代のように作図、製図の作業をあまりやっていないので平面図形に対するリアリティな感覚が弱い。だから、最初っから証明なんかやると心のシャッターが降りちゃう(^^;
そこで導入では、色半紙を三角形に切って持っていって折り紙をやります。「三角形の底辺の垂直二等分線を折って下さい」と言うと、半分くらいの生徒が「げっ」って顔をするんですが。「みんな知っているよ。大丈夫。よく考えてごらん」と粘ります。するとクラスのあちこちで声が出始めます。そのタイミングで「ほら三角形の底辺の頂点を合わせてしごいてみて」と言うとみんな「なぁんだ」。つかさず「他の二辺でもやってみて」、「上手な人は、1点で交わるよ」とあおります。今まで、何度かやりましたがいつも楽しそうにやってくれます。この手で垂心、重心、内心もできます。
6月の研究会 [研究会で]
放課後は、地区の数学教育の研究会に参加。参加者と日頃の授業での実践報告をかわした。私からは、数学Aは、集合・論理や場合の数より前に、平面図形を教えた方がうまく行くと報告、その中で平面図形も作図を中心にやった方が生徒たちは意欲的にやるとも報告した。他の参加者からも有意義な報告が色々出たが、一番インパクトがあったのが、因数分解の新しい指導法で、展開すると(X-Y+2)(X+3Y-4)=X^2+2XY-3Y^2(←ここまでは2次の項）-2X+10Y-8だから、もしX^2+2XY-3Y^2-2X+10Y-8を因数分解しようとすると2次の項だけを因数分解したとき（X-Y）（X+3Y）なので、=（X-Y+□）（X+3Y+□）の形にしか因数分解できない。後は、□にちょうどよい数を見つければ良いとの提案。これは、斬新なやり方だと納得。少なくとも教科書にのっている、Xの2次式と見なして、Yは数として扱ってたすきがけ等に持ち込む方法よりはずっと早いし簡単。いい勉強になった
